👷🏻 this is a work in progress 🔧

Sometimes by exploring incongruous ideas, one can make interesting discoveries. This is know as serendipity in science, with penicillin being a famous example of an unplanned discovery.

What I experimented with this week-end… is no such case. 😅
In the spirit of not holding back negative results though, and for the unlikely possibility that it turns out helpful for someone, I’ll share it regardless!

Too many dimensions

In computer vision we mostly deal with spatial data, so to make our life easier we often bake into the models the assumption that nearby elements are related. This is what the fundamental convolution operation give us in deep learning models, some bias towards spatial locality.

However not everything can be applied spatially, particularly on high dimensional spaces. For examples, building blocks designed for natural language processing often consider only one dimension. Even the transformer model, which is position independent in it’s original formulation, has been the focus of numerous researches attempting to bring back some locality, notably for efficiency improvements. Wouldn’t it be great to be able to use, as is, techniques developed for \(1D\) space on arbitrarily high \(ND\)?

The straightforward way to achieve it is to flatten whatever dimensions we have in order. For example, with a \(2D\) image we could take each row and concatenate them into a big list, and we’re done!
The issue is that we will break spatial locality. Neighboring pixels in a row will stay together, but pixel that were close within a column will suddenly have arbitrarily big distances separating them. Instead, we would like to flatten space while keeping the locality property as best as we can.

Space-filling curves to the rescue

Luckily, mathematicians have been studying this problem! I recommend this 3Blue1Brown for a great visual introduction, but in short the idea is to fill the entirety of space with a single curve.

There are a few different functions available, like the Peano and Hilbert curves, or most appropriate for us the Z-order curve (also known as Morton code). The advantage of the later is that, as illustrated in the figure above, on top of filling space it also preserve locality. Well, to an extent at least.

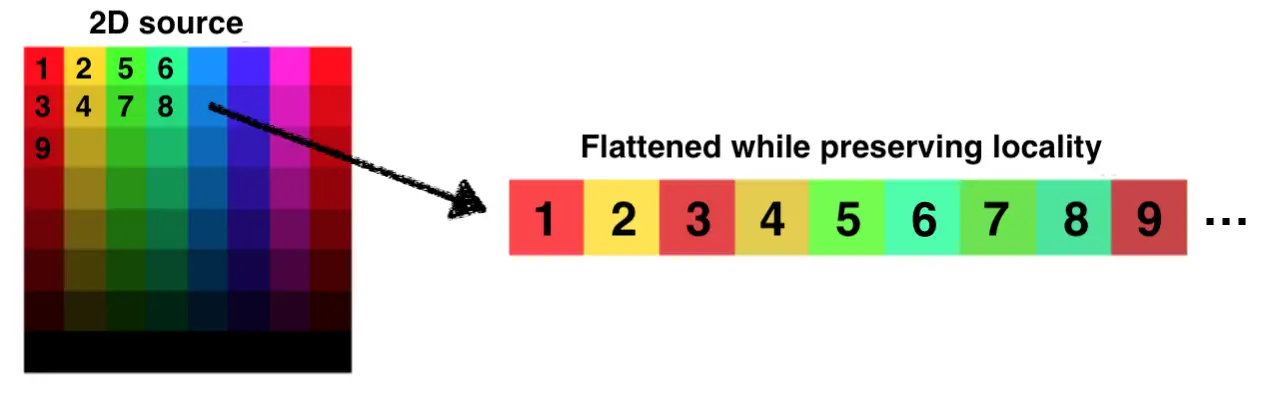
Using the Z-order function, we can create an index and use it for mapping from \(ND\) to \(1D\). Using einops to avoid getting lost in the dimensions, it is easy to create a function doing it for PyTorch.

(TODO: clean-up and publish the code)

Now that we have a way to flatten space while keeping some locality, we can design an experiment! To keep things fast I used the small CIFAR-10 dataset, which is fast enough to train on, even with a naive training loop implementation. As a bonus, I already had some code lying around that allowed me to reach 3000 samples/second on my aging 1070Ti (loosely based on Myrtle.ai posts about training speedup; a story for another time).

I tried 3 configurations:

• A baseline model with the usual 2D convolutions
• A model using 1D convolutions after flattening the input using the Z-order function
• The same 1D model but with naive flattening, and random flattening

All models are kept as close as possible, using the same 9-layers architecture and swapping the convolutions/batch-norm/pooling to either 2D or 1D.
Because convolving on lower dimensions use smaller kernels it result in less parameters, so I compensate by adjusting the layers' width until the number of trainable parameters match. While this is by no mean sufficient to make it an apple to apple comparison, it will have to do!

(TODO: finish the write-up :D)